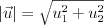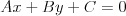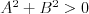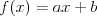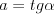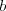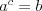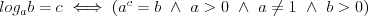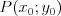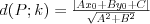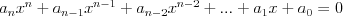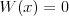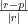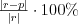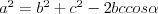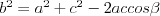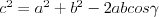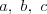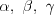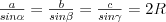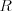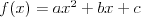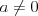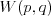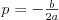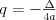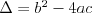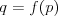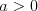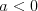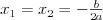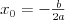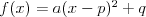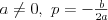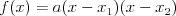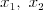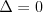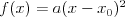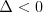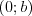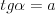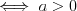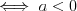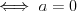Słownik zawiera pojęcia matematyczne występujące w programie szkoły ponadgimnazjalnej. Słownik jest w trakcie budowy, w miarę możliwości będzie uzupełniany .
Currently sorted By last update ascending Sort chronologically: By last update
CyfryCyfry - symbole służące do zapisywania liczb. Cyfry arabskie: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 - używane w dziesiątkowym systemie liczbowym (do Europy przenieśli je w X - XIII w. Arabowie, a wcześniej używali ich Hindusi). Cyfry rzymskie: I, V, X, L, C, D, M - pochodzenia latyno-etruskiego (VI - V w. p.n.e.). |
Ciąg geometryczny |
Liczby złożone Liczby złożone - liczby naturalne n > 1, które nie są liczbami pierwszymi, mają więc dzielnik naturalny k spełniający nierówność 1 < k < n. Twierdzenie: Każdą liczbę złożoną da się przedstawić w postaci iloczynu liczb pierwszych, przy czym rozkład na czynniki pierwsze jest jednoznaczny (tzn. dwa takie rozkłady mogą różnić się jedynie porządkiem czynników). |
Liczby pierwszeLiczby pierwsze - liczby naturalne p > 1, których jedynymi dzielnikami są liczby: 1 oraz p. Kolejnymi liczbami pierwszymi są: 2, 3, 5, 7, 11, 13, 17, 19, 23, ... . Istnieje nieskończenie wiele liczb pierwszych (udowodnił to w IV w.p.n.e matematyk grecki Euklides). |
Jednokładność Definicja: Jednokładnością o środku 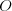 i skali i skali 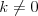 nazywamy takie przekształcenie płaszczyzny (przestrzeni), które każdemu punktowi nazywamy takie przekształcenie płaszczyzny (przestrzeni), które każdemu punktowi 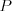 płaszczyzny (przestrzeni), przyporządkowuje taki punkt płaszczyzny (przestrzeni), przyporządkowuje taki punkt 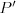 , taki że , taki że 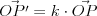 . .Własności jednokładności:
|
Pierwiastek wielomianu |
Pierwiastek k - krotny wielomianu Liczbę  nazywamy nazywamy 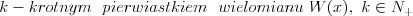 wtedy i tylko wtedy, gdy wielomian wtedy i tylko wtedy, gdy wielomian 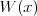 jest podzielny przez jest podzielny przez 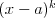 , ale nie jest podzielny przez , ale nie jest podzielny przez 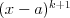 . Liczbę . Liczbę 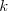 nazywamy krotnością pierwiastka. nazywamy krotnością pierwiastka. |
Symbol Newtona |
Wzory skróconego mnożenia |
Wielościan foremnyWielościanem foremnym (bryłą platońską) nazywamy wielościan wypukły, którego wszystkie ściany są przystającymi wielokątami foremnymi i każdy wierzchołek należy do takiej samej liczby ścian. Jest pięć rodzajów czworościanów foremnych:
|
RównoległościanRównoległościanem nazywamy graniastosłup, którego podstawą jest równoległobok. |
Ostrosłup prosty Definicja: Ostrosłupem prostym nazywamy ostrosłup spełniający dwa warunki:
Ostrosłup jest prosty  wszystkie jego krawędzie boczne mają jednakową długość. wszystkie jego krawędzie boczne mają jednakową długość.Twierdzenie 2: Ostrosłup jest prosty  wszystkie jego krawędzie boczne są nachylone do płaszczyzny podstawy pod tym samym kątem. wszystkie jego krawędzie boczne są nachylone do płaszczyzny podstawy pod tym samym kątem. |
Środek ciężkości... |
Twierdzenie o dwusiecznej kąta wewnętrznego trójkąta Dwusieczna kąta wewnętrznego trójkąta dzieli bok przeciwległy temu kątowi na dwa odcinki tak, że stosunek ich długości jest równy stosunkowi długości odpowiednich boków trójkąta, przyległych do tego kąta. |
Funkcja różnowartościowa | |
Okresowość funkcji... |
Funkcja parzysta |
Funkcja nieparzysta |
Monotoniczność funkcji... |
Zbiór wartości funkcji... |
Wzór Herona... |
Deltoid Deltoid - czworokąt wypukły, którego oś symetrii zawiera jedną z przekątnych. Deltoid ma dwie pary sąsiednich boków równych. Kąty deltoidu w wierzchołkach nie leżących na jego osi symetrii są przystające. Przekątne są prostopadłe, a ich punkt przecięcia jest środkiem przekątnej łączącej wierzchołki przystających kątów. |
Suma n początkowych wyrazów ciągu | |
Pochodna funkcji... |
Ciąg arytmetyczny |
Schemat Bernoulliego... |
Aksjomat Aksjomat - twierdzenie, którego prawdziwość przyjmuje się bez dowodu. |
Asymptota Asymptota funkcji - prosta o tej własności, że gdy punkt wykresu funkcji oddala się nieograniczenie po wykresie, to jego odległość od tej prostej dąży do zera. |
PermutacjeDefinicja Permutacją bez powtórzeń zbioru n-elementowego 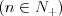 nazywamy każdy n-wyrazowy ciąg utworzony ze wszystkich elementów tego zbioru. nazywamy każdy n-wyrazowy ciąg utworzony ze wszystkich elementów tego zbioru. Twierdzenie Liczba 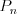 permutacji bez powtórzeń zbioru n-elementowego permutacji bez powtórzeń zbioru n-elementowego 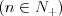 wyraża się wzorem: wyraża się wzorem: |
Wariacje z powtórzeniami... |
Wariacje bez powtórzeń.... |
Prawdopodobieństwo Definicja klasyczna prawdopodobieństwa Jeżeli przestrzeń 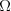 jest skończona i wszystkie zdarzenia elementarne tej przestrzeni są jednakowo prawdopodobne, to prawdopodobieństwo zajścia zdarzenia jest skończona i wszystkie zdarzenia elementarne tej przestrzeni są jednakowo prawdopodobne, to prawdopodobieństwo zajścia zdarzenia 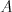 z tej przestrzeni (czyli z tej przestrzeni (czyli 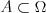 ) wyraża się wzorem ) wyraża się wzoremDefinicja aksjomatyczna Własności prawdopodobieństwa wkrótce...  | |
Funkcja homograficzna |
Wielomian Wielomianem stopnia  jednej zmiennej rzeczywistej jednej zmiennej rzeczywistej  nazywamy funkcję postaci: nazywamy funkcję postaci: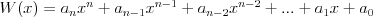 , gdzie , gdzie 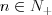 i i 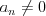 . .Liczby 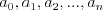 nazywamy współczynnikami wielomianu. nazywamy współczynnikami wielomianu.Wielomianem stopnia zerowego nazywamy funkcję stałą postaci: 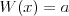 , gdzie , gdzie 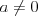 . .Wielomianem zerowym nazywamy funkcję stałą, przyjmującą dla każdego argumentu  wartość zero. Wielomian zerowy zapisujemy wartość zero. Wielomian zerowy zapisujemy 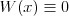 . .Pierwiastkiem wielomianu 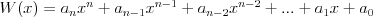 nazywamy jego miejsce zerowe, czyli każdą liczbę nazywamy jego miejsce zerowe, czyli każdą liczbę  , taką że , taką że 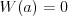 . .Twierdzenie Wielomian jednej zmiennej stopnia  posiada co najwyżej posiada co najwyżej  pierwiastków. pierwiastków. Twierdzenie Bezouta Liczba  jest pierwiastkiem wielomianu jest pierwiastkiem wielomianu 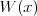  wielomian wielomian 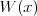 jest podzielny przez dwumian jest podzielny przez dwumian  . .Definicja Liczbę  nazywamy nazywamy 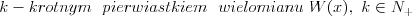 wtedy i tylko wtedy, gdy wielomian wtedy i tylko wtedy, gdy wielomian 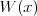 jest podzielny przez jest podzielny przez 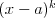 , ale nie jest podzielny przez , ale nie jest podzielny przez 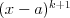 . Liczbę . Liczbę 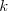 nazywamy krotnością pierwiastka. nazywamy krotnością pierwiastka. Twierdzenie Każdy wielomian o współczynnikach rzeczywistych można rozłożyć na czynniki co najwyżej drugiego stopnia o współczynnikach rzeczywistych. Twierdzenie Jeżeli liczby 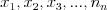 są pierwiastkami (niekoniecznie różnymi) wielomianu są pierwiastkami (niekoniecznie różnymi) wielomianu 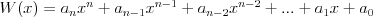 , gdzie , gdzie 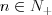 i i 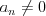 , to wielomian ten da się przedstawić w postaci iloczynowej: , to wielomian ten da się przedstawić w postaci iloczynowej: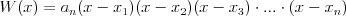 . . |
Równanie hiperboli | |
Hiperbola |
Koło | |
Graficzne rozwiązywanie równań, nierówności, układów Graficzne rozwiązywanie równań należy do tzw. metod przybliżonych, ponieważ metoda ta pozwala odczytać liczbę rozwiązań równania (układu), natomiast często nie da się odczytać ile to rozwiązanie dokładnie wynosi.
|
Równanie wymierne |
Równanie dwukwadratowe |
Miejsce zeroweMiejscem zerowym funkcji nazywany argument, dla którego funkcja przyjmuje wartość zero. |
Izometria Izometria - przekształcenie zachowujące odległość, tzn. takie, że odległość między punktami jest równa odległości między ich obrazami otrzymanymi w tym przekształceniu. Przykłady przekształceń izometrycznych (izometrii):
|
Równanie kwadratowe |
Rozkład wielomianu na czynniki Twierdzenie Każdy wielomian o współczynnikach rzeczywistych można rozłożyć na czynniki co najwyżej drugiego stopnia o współczynnikach rzeczywistych. Twierdzenie Jeżeli liczby 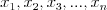 są pierwiastkami (niekoniecznie różnymi) wielomianu są pierwiastkami (niekoniecznie różnymi) wielomianu 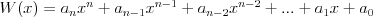 , gdzie , gdzie 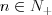 i i 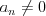 , to wielomian ten da się przedstawić w postaci iloczynowej: , to wielomian ten da się przedstawić w postaci iloczynowej: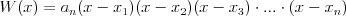 . .Sposoby rozkładu wielomianu na czynniki (najczęściej stosowane):
| |
Silnia |
Ciąg Ciągiem nazywamy funkcję, której dziedziną jest zbiór liczb naturalnych dodatnich 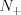 , lub skończony podzbiór początkowych liczb naturalnych dodatnich , lub skończony podzbiór początkowych liczb naturalnych dodatnich 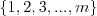 . . Wartości tej funkcji nazywamy wyrazami ciągu. Ciąg liczbowy to ciąg, którego wyrazy są liczbami rzeczywistymi. Gdy dziedziną ciągu jest 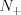 , to ciąg nazywamy nieskończonym, , to ciąg nazywamy nieskończonym,Gdy dziedziną ciągu jest 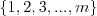 , to ciąg nazywamy skończonym (m-wyrazowym). , to ciąg nazywamy skończonym (m-wyrazowym).Sposoby opisywania ciągu: |
Równanie liniowe Równaniem liniowym z jedną niewiadomą  nazywamy równanie postaci nazywamy równanie postaci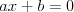 , gdzie , gdzie 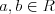 . .
|
Okrąg | |
Kombinacje |
Przestrzeń zdarzeń elementarnych Definicja Zbiorem zdarzeń elementarnych ( lub przestrzenią zdarzeń elementarnych) nazywamy zbiór wszystkich możliwych wyników doświadczenia losowego i oznaczamy 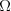 . .W matematyce szkolnej rozważamy tylko skończone zbiory zdarzeń elementarnych. 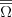 - oznacza liczbę elementów zbioru - oznacza liczbę elementów zbioru 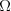 , czyli tzw. moc zbioru , czyli tzw. moc zbioru 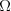 . .Definicja Zdarzeniem ( zdarzeniem losowym) nazywamy każdy podzbiór zbioru zdarzeń elementarnych. Zdarzenia oznaczamy najczęściej dużymi literami alfabetu: A, B, C, ... 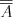 - oznacza liczbę elementów zbioru - oznacza liczbę elementów zbioru 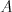 , czyli tzw. moc zbioru , czyli tzw. moc zbioru 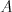 . . | |
Błąd bezwzględny Błędem bezwzględnym przybliżenia nazywamy wartość bezwzględną różnicy między wartością rzeczywistą (dokładną), a wartością przybliżoną (szacunkową), czyli jeśli: r - wartość rzeczywista p - wartość przybliżona, to |r-p| - błąd bezwzględny przybliżenia |
Zbiór liczb naturalnych | |
Największy wspólny dzielnikNajwiększym wspólnym dzielnikiem liczb a, b - w skrócie NWD(a,b) - nazywamy największą z liczb naturalnych, przez którą dzieli się bez reszty każda z liczb a, b. | |
Najmniejsza wspólna wielokrotność Najmniejszą wspólną wielokrotnością liczb a i b (a, b - liczby naturalne dodatnie) nazywamy najmniejszą liczbę naturalną różną od 0, która dzieli się bez reszty przez a i przez b. Najmniejszą wspólną wielokrotność liczb a i b i oznaczamy NWW(a,b). | |
Liczby względnie pierwsze Liczby naturalne są względnie pierwsze  ich jedynym wspólnym dzielnikiem naturalnym jest liczba 1, czyli: ich jedynym wspólnym dzielnikiem naturalnym jest liczba 1, czyli:Jeżeli a, b 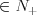 , to a, b - liczby względnie pierwsze , to a, b - liczby względnie pierwsze  NWD(a,b) = 1. NWD(a,b) = 1. |
Długość odcinka | |
Współrzędne wektora | |
Długość wektora | |
Równanie linii prostej |
Logarytm |
Odległość punktu od prostej |
Równanie wielomianoweRównanie n - tego stopnia z niewiadomą x (tzw. równanie wielomianowe) j.t. równanie postaci: | |
Błąd względny |
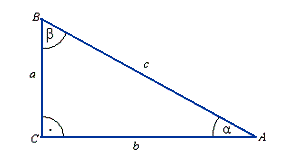
Twierdzenie cosinusów |
Twierdzenie sinusów |
Funkcja kwadratowaFunkcją kwadratową (trójmianem kwadratowym) nazywamy funkcję postaci
Postacie funkcji kwadratowej (wzajemnie równoważne): | |
Funkcja liniowa | |
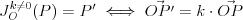
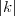
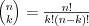
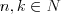
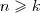
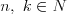
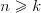
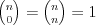
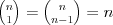
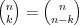
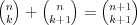
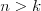
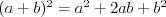
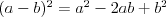
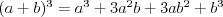
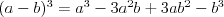
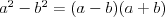
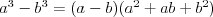
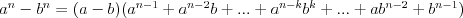
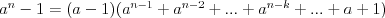
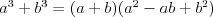
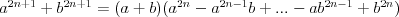
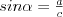
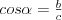
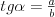
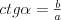
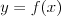
![\bigwedge\limits_{x_1,x_2\in {D_f}} [{x_1}\neq{x_2}\Rightarrow{f(x_1)}\neq{f(x_2)}] \bigwedge\limits_{x_1,x_2\in {D_f}} [{x_1}\neq{x_2}\Rightarrow{f(x_1)}\neq{f(x_2)}]](http://moodle.1lojaslo.pl/filter/tex/pix.php/a52bb4d55a40750c98e91c898b1984e9.png)
![\bigwedge\limits_{x\in {D_f}} [{-x\in{D_f}}\ \wedge\ f(-x)=f(x)] \bigwedge\limits_{x\in {D_f}} [{-x\in{D_f}}\ \wedge\ f(-x)=f(x)]](http://moodle.1lojaslo.pl/filter/tex/pix.php/5d2225f2d73e76889afc337019d4461c.png)
![\bigwedge\limits_{x\in {D_f}} [{-x\in{D_f}}\ \wedge\ f(-x)=-f(x)] \bigwedge\limits_{x\in {D_f}} [{-x\in{D_f}}\ \wedge\ f(-x)=-f(x)]](http://moodle.1lojaslo.pl/filter/tex/pix.php/0d347c806d331bf0e03481c6ce67825f.png)
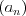
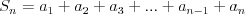
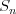
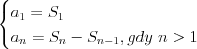

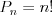
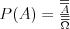
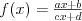
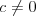
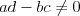
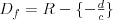
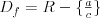
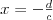
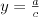
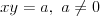
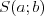
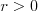
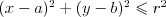
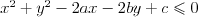
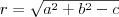
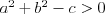
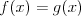
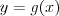
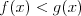
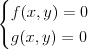
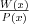
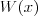
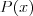
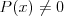
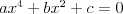
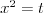
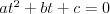
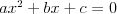
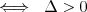
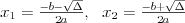
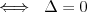
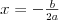
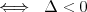
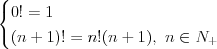
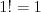
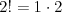
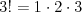

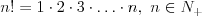
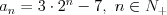
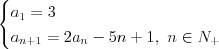
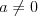
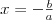
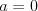
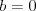
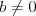
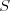
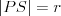
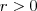

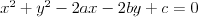
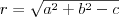
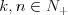
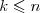
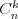
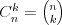
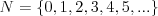
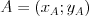
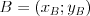
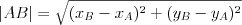
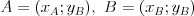
![\vec{AB}=[x_B-x_A;y_B-y_A] \vec{AB}=[x_B-x_A;y_B-y_A]](http://moodle.1lojaslo.pl/filter/tex/pix.php/51e26ed4dec2740f4afb26b66dd6a673.png)
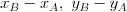
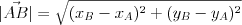
![\vec{u}=[u_1;u_2] \vec{u}=[u_1;u_2]](http://moodle.1lojaslo.pl/filter/tex/pix.php/26201e2455017bd6a48d8625b76b02b0.png)