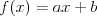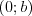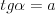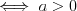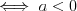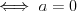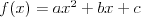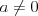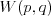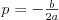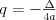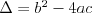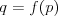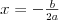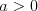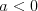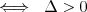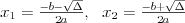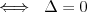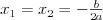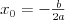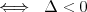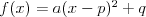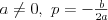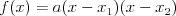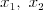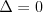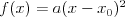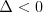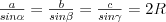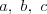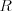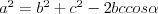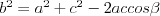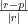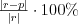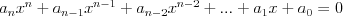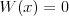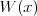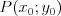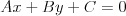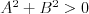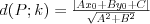Słownik zawiera pojęcia matematyczne występujące w programie szkoły ponadgimnazjalnej. Słownik jest w trakcie budowy, w miarę możliwości będzie uzupełniany .
Currently sorted By last update descending Sort chronologically: By last update
Funkcja liniowa | |
Twierdzenie sinusów |
Twierdzenie cosinusów |
Błąd względny |
Równanie wielomianoweRównanie n - tego stopnia z niewiadomą x (tzw. równanie wielomianowe) j.t. równanie postaci: | |
Odległość punktu od prostej |
CyfryCyfry - symbole służące do zapisywania liczb. Cyfry arabskie: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 - używane w dziesiątkowym systemie liczbowym (do Europy przenieśli je w X - XIII w. Arabowie, a wcześniej używali ich Hindusi). Cyfry rzymskie: I, V, X, L, C, D, M - pochodzenia latyno-etruskiego (VI - V w. p.n.e.). |
Ciąg geometryczny |
Liczby złożone Liczby złożone - liczby naturalne n > 1, które nie są liczbami pierwszymi, mają więc dzielnik naturalny k spełniający nierówność 1 < k < n. Twierdzenie: Każdą liczbę złożoną da się przedstawić w postaci iloczynu liczb pierwszych, przy czym rozkład na czynniki pierwsze jest jednoznaczny (tzn. dwa takie rozkłady mogą różnić się jedynie porządkiem czynników). |