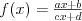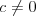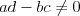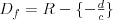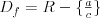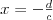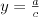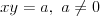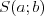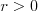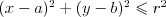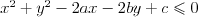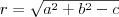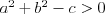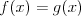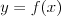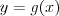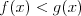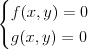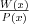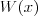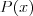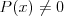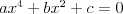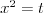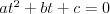Słownik zawiera pojęcia matematyczne występujące w programie szkoły ponadgimnazjalnej. Słownik jest w trakcie budowy, w miarę możliwości będzie uzupełniany .
Currently sorted By last update descending Sort chronologically: By last update
Funkcja homograficzna |
Wielomian Wielomianem stopnia  jednej zmiennej rzeczywistej jednej zmiennej rzeczywistej  nazywamy funkcję postaci: nazywamy funkcję postaci: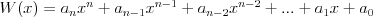 , gdzie , gdzie 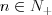 i i 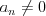 . .Liczby 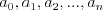 nazywamy współczynnikami wielomianu. nazywamy współczynnikami wielomianu.Wielomianem stopnia zerowego nazywamy funkcję stałą postaci: 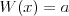 , gdzie , gdzie 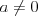 . .Wielomianem zerowym nazywamy funkcję stałą, przyjmującą dla każdego argumentu  wartość zero. Wielomian zerowy zapisujemy wartość zero. Wielomian zerowy zapisujemy 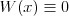 . .Pierwiastkiem wielomianu 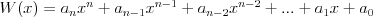 nazywamy jego miejsce zerowe, czyli każdą liczbę nazywamy jego miejsce zerowe, czyli każdą liczbę  , taką że , taką że 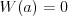 . .Twierdzenie Wielomian jednej zmiennej stopnia  posiada co najwyżej posiada co najwyżej  pierwiastków. pierwiastków. Twierdzenie Bezouta Liczba  jest pierwiastkiem wielomianu jest pierwiastkiem wielomianu 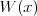  wielomian wielomian 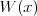 jest podzielny przez dwumian jest podzielny przez dwumian  . .Definicja Liczbę  nazywamy nazywamy 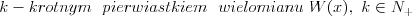 wtedy i tylko wtedy, gdy wielomian wtedy i tylko wtedy, gdy wielomian 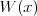 jest podzielny przez jest podzielny przez 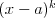 , ale nie jest podzielny przez , ale nie jest podzielny przez 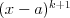 . Liczbę . Liczbę 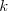 nazywamy krotnością pierwiastka. nazywamy krotnością pierwiastka. Twierdzenie Każdy wielomian o współczynnikach rzeczywistych można rozłożyć na czynniki co najwyżej drugiego stopnia o współczynnikach rzeczywistych. Twierdzenie Jeżeli liczby 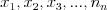 są pierwiastkami (niekoniecznie różnymi) wielomianu są pierwiastkami (niekoniecznie różnymi) wielomianu 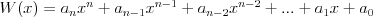 , gdzie , gdzie 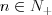 i i 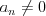 , to wielomian ten da się przedstawić w postaci iloczynowej: , to wielomian ten da się przedstawić w postaci iloczynowej: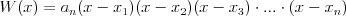 . . |
Równanie hiperboli | |
Hiperbola |
Koło | |
Równanie wymierne |
Równanie dwukwadratowe |
Miejsce zeroweMiejscem zerowym funkcji nazywany argument, dla którego funkcja przyjmuje wartość zero. |
Izometria Izometria - przekształcenie zachowujące odległość, tzn. takie, że odległość między punktami jest równa odległości między ich obrazami otrzymanymi w tym przekształceniu. Przykłady przekształceń izometrycznych (izometrii):
|