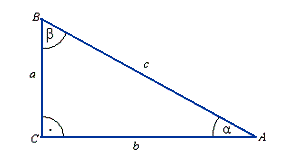
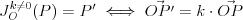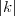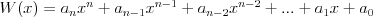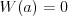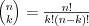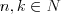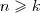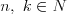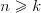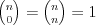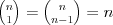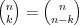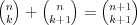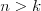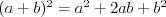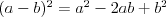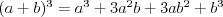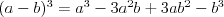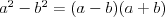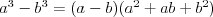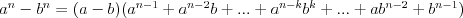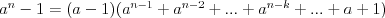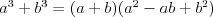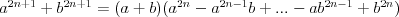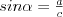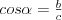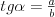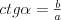Słownik zawiera pojęcia matematyczne występujące w programie szkoły ponadgimnazjalnej. Słownik jest w trakcie budowy, w miarę możliwości będzie uzupełniany .
Currently sorted By last update descending Sort chronologically: By last update
Liczby pierwszeLiczby pierwsze - liczby naturalne p > 1, których jedynymi dzielnikami są liczby: 1 oraz p. Kolejnymi liczbami pierwszymi są: 2, 3, 5, 7, 11, 13, 17, 19, 23, ... . Istnieje nieskończenie wiele liczb pierwszych (udowodnił to w IV w.p.n.e matematyk grecki Euklides). |
Jednokładność Definicja: Jednokładnością o środku  i skali i skali 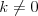 nazywamy takie przekształcenie płaszczyzny (przestrzeni), które każdemu punktowi nazywamy takie przekształcenie płaszczyzny (przestrzeni), które każdemu punktowi  płaszczyzny (przestrzeni), przyporządkowuje taki punkt płaszczyzny (przestrzeni), przyporządkowuje taki punkt 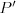 , taki że , taki że 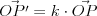 . .Własności jednokładności:
|
Pierwiastek wielomianu |
Pierwiastek k - krotny wielomianu Liczbę  nazywamy nazywamy 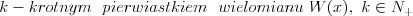 wtedy i tylko wtedy, gdy wielomian wtedy i tylko wtedy, gdy wielomian 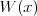 jest podzielny przez jest podzielny przez 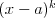 , ale nie jest podzielny przez , ale nie jest podzielny przez 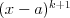 . Liczbę . Liczbę 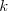 nazywamy krotnością pierwiastka. nazywamy krotnością pierwiastka. |
Symbol Newtona |
Wzory skróconego mnożenia |
Wielościan foremnyWielościanem foremnym (bryłą platońską) nazywamy wielościan wypukły, którego wszystkie ściany są przystającymi wielokątami foremnymi i każdy wierzchołek należy do takiej samej liczby ścian. Jest pięć rodzajów czworościanów foremnych:
|
RównoległościanRównoległościanem nazywamy graniastosłup, którego podstawą jest równoległobok. |
Ostrosłup prosty Definicja: Ostrosłupem prostym nazywamy ostrosłup spełniający dwa warunki:
Ostrosłup jest prosty  wszystkie jego krawędzie boczne mają jednakową długość. wszystkie jego krawędzie boczne mają jednakową długość.Twierdzenie 2: Ostrosłup jest prosty  wszystkie jego krawędzie boczne są nachylone do płaszczyzny podstawy pod tym samym kątem. wszystkie jego krawędzie boczne są nachylone do płaszczyzny podstawy pod tym samym kątem. |