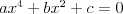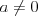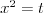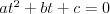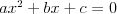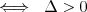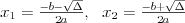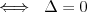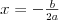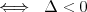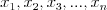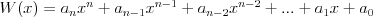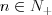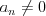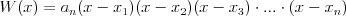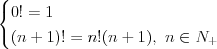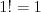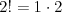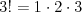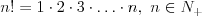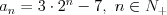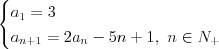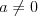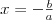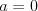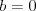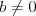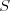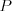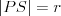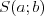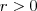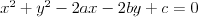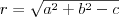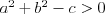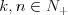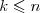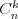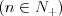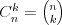Słownik zawiera pojęcia matematyczne występujące w programie szkoły ponadgimnazjalnej. Słownik jest w trakcie budowy, w miarę możliwości będzie uzupełniany .
Currently sorted By last update ascending Sort chronologically: By last update
Równanie dwukwadratowe |
Miejsce zeroweMiejscem zerowym funkcji nazywany argument, dla którego funkcja przyjmuje wartość zero. |
Izometria Izometria - przekształcenie zachowujące odległość, tzn. takie, że odległość między punktami jest równa odległości między ich obrazami otrzymanymi w tym przekształceniu. Przykłady przekształceń izometrycznych (izometrii):
|
Równanie kwadratowe |
Silnia |
Ciąg Ciągiem nazywamy funkcję, której dziedziną jest zbiór liczb naturalnych dodatnich 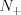 , lub skończony podzbiór początkowych liczb naturalnych dodatnich , lub skończony podzbiór początkowych liczb naturalnych dodatnich 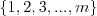 . . Wartości tej funkcji nazywamy wyrazami ciągu. Ciąg liczbowy to ciąg, którego wyrazy są liczbami rzeczywistymi. Gdy dziedziną ciągu jest 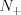 , to ciąg nazywamy nieskończonym, , to ciąg nazywamy nieskończonym,Gdy dziedziną ciągu jest 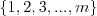 , to ciąg nazywamy skończonym (m-wyrazowym). , to ciąg nazywamy skończonym (m-wyrazowym).Sposoby opisywania ciągu: |
Równanie liniowe Równaniem liniowym z jedną niewiadomą  nazywamy równanie postaci nazywamy równanie postaci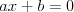 , gdzie , gdzie 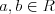 . .
|
Okrąg | |
Kombinacje |